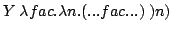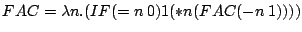
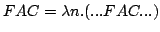
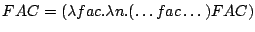
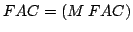
where:
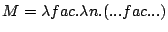
The recursion is eliminated by enclosing the recursive function in a lambda abstraction, that receives the function to be invoked recursively as an argument.
Therefore we can write:
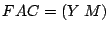
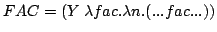
((
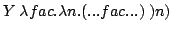
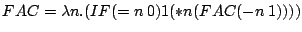
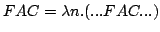
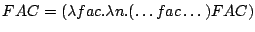
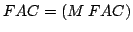
where:
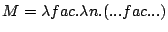
The recursion is eliminated by enclosing the recursive function in a lambda abstraction, that receives the function to be invoked recursively as an argument.
Therefore we can write:
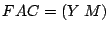
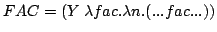
((